Entender juros compostos muda a forma como você enxerga dinheiro, porque mostra que o tempo pode trabalhar a seu favor quando você investe com constância, ou contra você quando uma dívida cresce silenciosamente a cada mês.
Ao dominar a lógica do “juros sobre juros”, você aprende por que um pequeno percentual se transforma em um grande resultado quando multiplicado por muitos períodos, compreende como comparar cenários de taxa e prazo e ganha autonomia para simular metas, parcelamentos, aportes mensais e o montante futuro que cada decisão produz, tudo com uma linguagem clara, exemplos passo a passo e analogias que tiram a matemática do pedestal sem perder a precisão.
Neste guia, você terá uma explicação fácil de juros compostos com números reais, verá uma mini calculadora para usar no celular, aprenderá a construir gráficos simples para visualizar a curva de crescimento, praticará com exercícios comentados e conhecerá um glossário direto ao ponto, para que a teoria vire ferramenta prática no seu dia a dia financeiro.
Aviso de independência: este conteúdo é educacional, não substitui aconselhamento individual, e não contém links; adapte as contas à sua realidade de taxa, prazo, impostos e custos.
Juros compostos, em uma imagem mental que não sai da cabeça
Imagine uma bola de neve descendo uma montanha, que não apenas rola, mas carrega na superfície mais neve a cada volta, aumentando o próprio diâmetro e, com isso, ganhando ainda mais neve na volta seguinte; juros compostos funcionam exatamente assim, porque os juros de um período são incorporados ao principal, gerando novos juros sobre uma base maior no período seguinte.
Pense também em uma planta que recebe água e luz com regularidade: no começo, o crescimento parece lento, porém, com o passar das semanas, os galhos multiplicam folhas e as folhas multiplicam brotos, criando um efeito cumulativo; o dinheiro, quando recebe tempo e taxa, germina como um organismo vivo que se alimenta de sua própria expansão.
A fórmula que está por trás do “juros sobre juros”, sem rodeios
A matemática por trás dos juros compostos cabe em uma linha, e entender o papel de cada pedaço facilita todas as simulações que você fará a seguir.
- Montante (M): valor final depois de n períodos.
- Capital (C): valor inicial aplicado ou devido.
- Taxa (i): percentual por período (ao mês, ao ano, ao dia), na forma decimal.
- Períodos (n): quantidade de vezes que a taxa incide.
A relação entre essas variáveis é:
M = C × (1 + i)ⁿ
- Quando existe aporte mensal adicional, entra o segundo termo da soma:
M = C × (1 + i)ⁿ + A × [((1 + i)ⁿ − 1) / i]
onde A é o valor do aporte periódico na mesma frequência da taxa.

Mini calculadora de juros compostos no celular, sem apps extras
- Escolha a base de tempo igual para taxa e períodos: se a taxa é ao mês, os períodos são em meses; se a taxa é ao ano, os períodos são em anos.
- Transforme a taxa em decimal: 1% vira 0,01; 0,8% vira 0,008; 12% ao ano vira 0,12.
- Use o modo científico da calculadora: digite
(1 + i)e utilize a teclaxʸpara elevar à potêncian. - Multiplique pelo capital para obter o montante, e subtraia o capital do montante para ver os juros.
- Inclua aportes mensais quando existirem, multiplicando o fator de soma
[((1 + i)ⁿ − 1)/i]pelo valor do aporte e, por fim, somando ao montante do capital inicial.
Exemplos numéricos passo a passo, com contas transparentes
Exemplo 1 — Montante de R$ 1.000 a 1% ao mês por 12 meses (sem aporte)
- Dados: C = 1.000, i = 0,01 ao mês, n = 12.
- Cálculo do fator: (1,01)¹² ≈ 1,126825.
- Montante: M = 1.000 × 1,126825 ≈ R$ 1.126,83.
- Juros: J = 1.126,83 − 1.000 = R$ 126,83.
Observe que os juros do mês seguinte incidem sobre 1.010, depois sobre 1.020,10, e assim por diante, criando a “bola de neve”.
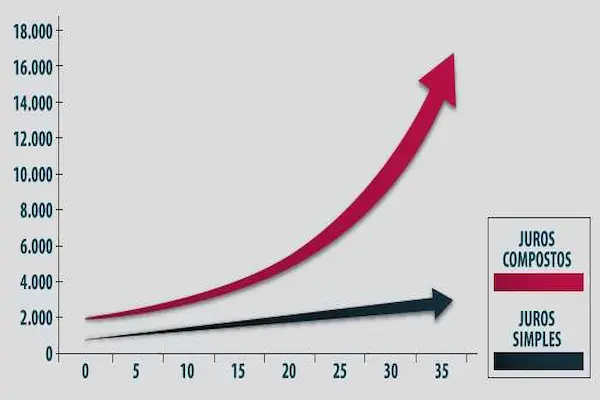
Exemplo 2 — Comparação com juros simples nas mesmas condições
- Juros simples: M = 1.000 × (1 + 0,01 × 12) = 1.000 × 1,12 = R$ 1.120,00.
- Diferença: 1.126,83 − 1.120,00 = R$ 6,83 a mais em 12 meses.
Parece pouco em um ano, porém a diferença explode quando você aumenta o prazo ou a taxa, como você verá a seguir.
Exemplo 3 — A força do tempo: 1% ao mês por 60 meses
- Fator: (1,01)⁶⁰ ≈ 1,8167.
- Montante: 1.000 × 1,8167 ≈ R$ 1.816,70.
- Juros: R$ 816,70.
Com o dobro do tempo, os juros não dobram; eles crescem muito mais, pois a base aumenta a cada período.
Exemplo 4 — A força da taxa: 2% ao mês por 12 meses
- Fator: (1,02)¹² ≈ 1,26824.
- Montante: 1.000 × 1,26824 ≈ R$ 1.268,24.
- Juros: R$ 268,24.
Dobrar a taxa mais que dobra os juros no mesmo prazo, e essa sensibilidade explica por que dívidas caras viram problemas rápidos.
Exemplo 5 — Dívida no cartão: 12% ao mês por 6 meses (sem pagamento)
- Fator: (1,12)⁶ ≈ 1,9738.
- Montante: 1.000 × 1,9738 ≈ R$ 1.973,80.
- Juros: R$ 973,80 em meio ano.
O rotativo do cartão transforma uma quantia modesta em quase o dobro, ilustração perfeita de como juros compostos também são perigosos quando atuam contra você.
Exemplo 6 — Com aportes mensais: R$ 1.000 iniciais + R$ 200 por mês a 1% ao mês por 24 meses
- Fator de capital: (1,01)²⁴ ≈ 1,26824.
- Montante sobre o capital: 1.000 × 1,26824 = R$ 1.268,24.
- Fator de soma dos aportes:
[(1,01)²⁴ − 1] / 0,01≈ (1,26824 − 1) / 0,01 ≈ 26,824. - Montante dos aportes: 200 × 26,824 ≈ R$ 5.364,80.
- Total: R$ 6.633,04.
Combinar tempo, taxa e aportes regulares explica por que constância vence pressa em finanças pessoais.
Gráficos ilustrativos com dados de verdade (versão tabela e “gráfico de barras” em texto)
Quando não dá para inserir imagens, uma tabela bem montada e um gráfico de barras em texto ajudam a visualizar a curva.
Crescimento mês a mês — R$ 1.000 a 1% ao mês (12 meses)
| Mês | Montante (R$) |
|---|---|
| 0 | 1.000,00 |
| 1 | 1.010,00 |
| 2 | 1.020,10 |
| 3 | 1.030,30 |
| 4 | 1.040,60 |
| 5 | 1.051,01 |
| 6 | 1.061,52 |
| 7 | 1.072,14 |
| 8 | 1.082,86 |
| 9 | 1.093,69 |
| 10 | 1.104,62 |
| 11 | 1.115,67 |
| 12 | 1.126,83 |
“Barras” proporcionais (quanto maior o número, maior a barra)
- Mês 0: ██████████ 1.000
- Mês 6: ████████████ 1.061
- Mês 12: █████████████ 1.126
Note como a distância entre barras cresce ligeiramente ao longo do tempo, evidenciando a aceleração típica do composto.
Regra dos 72 e o atalho para estimar duplicação do capital
A regra dos 72 é um truque mental que aproxima o tempo necessário para dobrar um valor sob juros compostos: divida 72 pela taxa em % no mesmo período.
- Exemplo: a 1% ao mês, 72 ÷ 1 ≈ 72 meses (~6 anos).
- Exemplo: a 12% ao ano, 72 ÷ 12 = 6 anos.
A regra não é exata, porém erra pouco em taxas moderadas, e ajuda a criar senso de grandeza sem tirar a calculadora do bolso.
Taxa nominal x taxa efetiva e a conversão de períodos, sem confusão
Muita gente confunde 1% ao mês com 12% ao ano, mas em composição esses números não são equivalentes, porque a taxa anual efetiva precisa considerar a capitalização mensal.
- Conversão de mensal para anual (efetiva):
(1 + i_mensal)¹² − 1. - Exemplo: 1% ao mês → (1,01)¹² − 1 ≈ 12,6825% ao ano.
- Conversão de anual para mensal (efetiva):
(1 + i_anual)^(1/12) − 1. - Exemplo: 12% ao ano → (1,12)^(1/12) − 1 ≈ 0,949% ao mês.
Esclarecer a periodicidade é metade do trabalho para comparar propostas de investimento ou financiamento.
Valor presente: quanto preciso hoje para alcançar um montante futuro
Quando o objetivo é descobrir quanto investir hoje para ter um valor no futuro sob uma taxa, usa-se o desconto composto.
- Fórmula:
C = M / (1 + i)ⁿ. - Exemplo: para alcançar R$ 10.000 em 36 meses a 0,8% ao mês:
Fator (1,008)³⁶ ≈ 1,332.
Capital necessário: 10.000 / 1,332 ≈ R$ 7.507.
A lógica é a inversa da multiplicação, porque você “traz o futuro para o presente”.
Como montar um gráfico no Excel/Google Sheets em 3 minutos
- Monte a lista de meses em uma coluna, de 0 a n.
- Calcule o montante em outra coluna usando
=C*(1+i)^mês. - Selecione as duas colunas e insira um gráfico de linhas.
- Ajuste o título (“Crescimento com Juros Compostos”) e formate valores com duas casas decimais.
- Crie séries comparativas duplicando a coluna com outra taxa e mudando apenas o
i, para ver a diferença visual entre 0,5% e 1%, por exemplo.
Erros comuns que atrapalham a compreensão, com correções simples
- Misturar taxa nominal com efetiva: compare sempre taxas em mesma base e, se necessário, converta pela fórmula correta.
- Ignorar impostos e taxas de administração: simule o rendimento líquido, abatendo custos para não superestimar o montante.
- Confundir período da taxa: taxa ao ano com período em meses dá resultado errado; alinhe sempre as unidades.
- Subestimar o poder do tempo: desistir cedo corta a parte mais inclinada da curva; constância é mais importante que grandes aportes isolados.
- Aplicar a fórmula errada para aportes: aporte mensal usa a fórmula da série de pagamentos; não some juros simples sobre cada aporte.
Exercícios práticos (do básico ao aplicado)
Exercício 1 — Montante simples sem aportes
Calcule o montante de R$ 5.000 a 0,8% ao mês por 18 meses.
Peça: montante e juros.
Exercício 2 — Compara simples x composto
Quanto vira R$ 2.000 a 1,5% ao mês por 10 meses em juros simples e em juros compostos, e qual a diferença entre os montantes?
Exercício 3 — Tempo para dobrar
Usando a regra dos 72 e o cálculo exato, estime quantos meses são necessários para dobrar um valor a 0,8% ao mês.
Exercício 4 — Aportes mensais
Sem capital inicial, qual o montante ao investir R$ 400 por mês a 0,7% ao mês por 24 meses?
Exercício 5 — Quanto devo aportar para atingir uma meta
Qual deve ser o aporte mensal para alcançar R$ 15.000 em 36 meses a 0,5% ao mês, partindo de zero?
Exercício 6 — Valor presente
Qual o capital hoje necessário para ter R$ 10.000 em 36 meses a 0,8% ao mês?
Gabarito no final deste artigo.
Glossário rápido, sem jargão
- Capital (C): valor inicial investido ou devido.
- Montante (M): valor final após os juros e os aportes.
- Taxa (i): percentual por período, em decimal na fórmula.
- Período (n): número de vezes que a taxa incide.
- Juros compostos: juros calculados sobre capital + juros acumulados.
- Juros simples: juros calculados apenas sobre o capital inicial.
- Valor presente: o que hoje equivale a um montante futuro considerando uma taxa.
- Série de pagamentos: sequência de aportes iguais em intervalos regulares, usada para calcular montantes com aportes mensais.
- Taxa nominal: percentual anunciado sem considerar a capitalização.
- Taxa efetiva: percentual real após considerar como a taxa se compõe no período.
Tabelas-resumo que agilizam a vida
Fatores aproximados para 1% ao mês
| Meses | (1,01)ⁿ |
|---|---|
| 6 | 1,0615 |
| 12 | 1,1268 |
| 24 | 1,2682 |
| 36 | 1,4258 |
| 60 | 1,8167 |
Conversão de taxa mensal para anual (efetiva)
- 0,5% a.m → (1,005)¹² − 1 ≈ 6,17% a.a.
- 0,8% a.m → (1,008)¹² − 1 ≈ 9,97% a.a.
- 1,0% a.m → (1,01)¹² − 1 ≈ 12,68% a.a.
- 1,5% a.m → (1,015)¹² − 1 ≈ 19,56% a.a.
Passos numerados para usar a fórmula com segurança todas as vezes
- Escolha a base: confirme se a taxa é ao mês ou ao ano, e traga os períodos para a mesma base.
- Converta a taxa: passe de porcentagem para decimal.
- Calcule o fator: compute
(1 + i)ⁿno modo científico da calculadora. - Aplique ao capital: multiplique o fator por C para obter M.
- Inclua aportes: se houver contribuições regulares, calcule
A × [((1 + i)ⁿ − 1) / i]e some ao montante do capital. - Cheque plausibilidade: reflita se o resultado faz sentido comparando com um “chute” aproximado (regra dos 72, por exemplo).
- Registre e compare: anote os cenários, troque uma variável por vez (taxa, prazo, aporte) e observe o impacto.
Roteiro de estudo em 7 dias para fixar a ideia sem sofrimento
- Dia 1: leia a explicação e resolva o Exercício 1.
- Dia 2: construa a planilha com a fórmula e replique o Exemplo 1.
- Dia 3: plote um gráfico de linhas com taxas de 0,5% e 1% a.m.
- Dia 4: faça o Exercício 2 e compare simples versus composto.
- Dia 5: simule aportes mensais e refaça o Exemplo 6 com seus números.
- Dia 6: converta taxas mensais em anuais e vice-versa.
- Dia 7: resolva os Exercícios 3 a 6 e confira o gabarito.
Aplicações do dia a dia: quando usar juros compostos do lado certo
- Reserva e objetivos: ao automatizar um pequeno aporte mensal, você ativa o composto a seu favor, principalmente quando ganha tempo de capitalização.
- Planejamento de grandes compras: simular o montante futuro evita financimentos caros e favorece o pagamento à vista com desconto.
- Análise de dívidas: ao perceber a taxa efetiva mensal e anual, fica mais fácil priorizar o que deve ser quitado primeiro.
- Comparação de propostas: trazer todas as taxas para a mesma base e capitalização transforma “achismos” em decisão com fundamento.

Gabarito dos exercícios
Exercício 1
Fator (1,008)¹⁸ ≈ 1,154.
Montante: 5.000 × 1,154 ≈ R$ 5.770,00.
Juros: R$ 770,00.
Exercício 2
Simples: 2.000 × (1 + 0,015 × 10) = 2.000 × 1,15 = R$ 2.300,00.
Composto: 2.000 × (1,015)¹⁰ ≈ 2.000 × 1,160 ≈ R$ 2.320,00.
Diferença: R$ 20,00.
Exercício 3
Regra dos 72: 72 ÷ 0,8 = 90 meses.
Cálculo exato: n = ln(2)/ln(1,008) ≈ 0,6931/0,007968 ≈ 86,95 meses.
Exercício 4
Fator (1,007)²⁴ ≈ 1,183.
Soma dos aportes: ((1,183 − 1)/0,007) ≈ 26,14.
Montante: 400 × 26,14 ≈ R$ 10.456,00 (aprox.).
Exercício 5
Aporte A = Meta × i / ((1 + i)ⁿ − 1).
A = 15.000 × 0,005 / ((1,005)³⁶ − 1).
Fator (1,005)³⁶ ≈ 1,19668; denominador ≈ 0,19668.
A ≈ 75 / 0,19668 ≈ R$ 381,30 (arredonde para R$ 382).
Exercício 6
Valor presente: C = 10.000 / (1,008)³⁶ ≈ 10.000 / 1,332 ≈ R$ 7.507.
Tempo, taxa e constância formam o tripé dos juros compostos
Quando você compreende que a taxa multiplica a base e que o tempo multiplica o efeito da taxa, fica claro que a constância de aportes multiplica o resultado de ambos, razão pela qual o “comece pequeno e cedo” vence o “comece grande e tarde”, sobretudo em finanças pessoais onde disciplina pesa mais que genialidade.
Ao levar consigo uma explicação fácil, uma mini calculadora mental e uma rotina de simular cenários, você passa a decidir com mais serenidade porque enxerga o futuro com números, e não com palpites; use as fórmulas para investir melhor, para evitar dívidas caras, para comparar propostas de crédito e para alinhar expectativas com prazos realistas, lembrando que a parte mais bonita do composto aparece justamente nos períodos mais longos, que só existem para quem persiste.